Robust machine vision systems are frequently required to recognize targets of unknown scale, unknown position and unknown rotation. In general, any solution to this difficult problem will require that the input imagery be somehow constrained. In industrial machine vision applications, the camera position can be fixed, there is usually a limited number of variations on the object to recognize, and the lighting conditions can be fixed if the system is enclosed. With systems such as this in place, 2D intensity images can be thresholded to yield images typified by figure 2.
By thresholding an image, we seek to eliminate all information except for the general shape of an observed object. From these thresholded silhouette images, referred to as blobs, one observes the low frequency components of the imaged blob: size, orientation, and low-level shape. By edge processing the image, the high frequency detail of the blob's bounding contour is revealed. Figure 3 shows the result of a thresholded 3x3 optimized Sobel edge operation on the blob image.
In Visual Pattern Recognition by Moment Invariants[3], Hu derives a set of seven functions that make use of the central moments of a blob image; their output is independent of any translation, rotation or mirror image of a particular blob, and they can be used in conjunction with both the blob image itself and the edge-processed contour image. All the images in figure 4 accurately produce the same numerical result for each of Hu's seven equations.
Hu's equations are based on the uniqueness theory of moments. For a
digital image of size (N,M) the p+qth order moments mpq are
calculated, (for
![]() )
)
The uniqueness theorem of moments: The infinite sequence of moments mpq is uniquely determined by the joint function f(x,y); conversely, the function f(x,y) is uniquely determined by an infinite sequence of moments mpq. Strictly, this is only valid for continuous functions whose value is zero wherever x,y are not finite. In general, gross image shape is represented well by the lower-order moments, and high-order moments only reflect the subtleties of a silhouette or boundary image. Nearly all work with moment invariants, including Hu's, depends only on moments of order zero to three.
The central moments of a digital blob image are inherently translation independent,
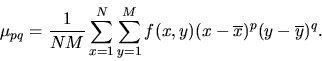 |
(2) |
Where
![]() and
and
![]() .
Hu's seven moment functions below utilize the central
moments of a digital silhouette or boundary image, but are also
rotation independent (equations 3 to 9).
.
Hu's seven moment functions below utilize the central
moments of a digital silhouette or boundary image, but are also
rotation independent (equations 3 to 9).
M1 through M6 are all translation and rotation independent for digital images, but M7 is actually skew invariant - its sign can be used to detect mirror images.
In a paper by Dudani, Breeding, and McGhee[2], Hu's
equations above were expanded to act nearly scale-invariant. Using
the radius of gyration of a planar pattern,
![]() ,
the equations can be normalized so that they remain
unaffected by the size of the blob or edge boundary in the digital
image:
,
the equations can be normalized so that they remain
unaffected by the size of the blob or edge boundary in the digital
image:
| M1' | = | (10) | |
| M2' | = | M2/r4 | (11) |
| M3' | = | M3/r6 | (12) |
| M4' | = | M4/r6 | (13) |
| M5' | = | M5/r12 | (14) |
| M6' | = | M6/r8 | (15) |
| M7' | = | M7/r12 | (16) |
For this paper, M1' will not be used because it requires that the distance from the camera to the observed object, B, is known.
When designing a classifier, either set of above relations can be
packed into a seven-dimensional feature vector
![]() .
In this high-dimensional space, groups of
feature vectors corresponding to particular silhouette blob or edge
boundary images can be easily separated by splitting the space with
hyperplanes or other high-dimensional surfaces. In practice, as will
be shown in the following section, one may not even need all seven
moment invariant functions to design a classifier.
.
In this high-dimensional space, groups of
feature vectors corresponding to particular silhouette blob or edge
boundary images can be easily separated by splitting the space with
hyperplanes or other high-dimensional surfaces. In practice, as will
be shown in the following section, one may not even need all seven
moment invariant functions to design a classifier.